The GLOBEC Kriging Software Package
EasyKrig3.0 July 15, 2004
Copyright (c) 1998, 2001, 2004 property of
Dezhang Chu and Woods Hole Oceanographic Institution. All Rights Reserved.
The kriging software described in this document
was developed by Dezhang Chu with funding from the National Science Foundation
through the U.S. GLOBEC Georges Bank Project's Program Service and Data
Management Office. It was originally inspired by a MATLAB toolbox developed by
Yves Gratton and Caroline Lafleur (INRS-Oceanologie, Rimouski, Qc, Canada), and
Jeff Runge (Institut Maurice-Lamontagne, now with University of New Hampshire).
This software may be reproduced for noncommercial purposes only.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY. Contact Dr. Chu at dchu@whoi.edu with enhancements or suggestions for changes.
For a Czech translation of the documentation for the Version 2.1 of the program, click here (Translation by Barbora Lebedová).
For a Georgian translation of this document, click here. (Contributed by Irakli Nishnianidze)
For an Indonesian translation of this document, click here.
For a Polish translation of this document, click here. (Contributed by Valeria Aleksandrova)
For a Romanian translation of the documentation for Version 2.1 of the program, click here. (Translation by Paula-Maria Niculescu).
For a Ukrainian translation of this document, click here. (Translation by Mikalay Lisica)
For a Russian translation of this document, click here.
Table
of Contents:
1. Introduction
1.1 General
Information
1.1.1 About kriging
1.1.2 Brief
descriptions of easy_krig3.0
1.2 Getting started
1.2.1 Operating systems
1.2.2 Down-load the
program
1.2.3 Quick start
2. Data Processing Stages
2.1 Data Preparation
2.2 Semi-variogram
2.3 Kriging
2.4 Visualization
2.5
Saving
Kriging Results
3. Examples
3.1 Example 1: An Aerial Image of Zooplankton Abundance Data
3.2 Example 2: A Vertical Section of Salinity Data: An
Anisotropic Data set
3.3 Example 3: Batch Process of
Pressure (dbar) at Different Potential Density Layers
3.4 Example 4: 3-Dimensional
Temperature Data
4. References
1.
Introduction
1.1
General Information
1.1.1
About kriging
This section provides a brief theoretical background
for kriging. If the user(s) is not interested in the theoretical background,
he/she can skip this section and go to section 1.1.2 directly.
Kriging
is a technique that provides the Best Linear Unbiased Estimator of the unknown
fields (Journel and Huijbregts, 1978; Kitanidis, 1997). It is a local estimator that can provide the
interpolation and extrapolation of the originally sparsely sampled data that
are assumed to be reasonably characterized by the Intrinsic Statistical Model
(ISM). An ISM does not require the quantity of interest to be stationary, i.e.
its mean and standard deviation are independent of position, but rather that
its covariance function depends on the separation of two data points only, i.e.
E[ (z(x) - m)(z(x' - m) ]
= C(h), (1)
where m is
the mean of z(x) and C(h)
is the covariance function with lag h, with h being the distance
between two samples x and x':
h = || x - x'|| = ![]() (2)
(2)
Another
way to characterize an ISM is to use a semi-variogram,
![]() = 0.5* E[ (z(x) - (x'))2]. (3)
= 0.5* E[ (z(x) - (x'))2]. (3)
The relation between the
covariance function and the semi-variogram is
![]() = C(0) - C(h). (4)
= C(0) - C(h). (4)
The
kriging method is to find a local estimate of the quantity at a
specified location, ![]() . This estimate
is a weighted average of the N adjacent observations:
. This estimate
is a weighted average of the N adjacent observations:
![]() (5)
(5)
The
weighting coefficients ![]() can be determined based on the minimum
estimation variance criterion:
can be determined based on the minimum
estimation variance criterion:
![]() (6)
(6)
subject to
the normalization condition
![]() . (7)
. (7)
Note
that we don't know the exact value at ![]() , but we are
trying to find a predicted value that provides the minimum estimation variance.
The resultant kriging equation can be expressed as
, but we are
trying to find a predicted value that provides the minimum estimation variance.
The resultant kriging equation can be expressed as
 (8)
(8)
where µ
is the Lagrangian coefficient. In addition, we have replaced the covariance
function with the normalized covariance function [normalized by C(0)].
Equivalently, by using Eq. (4), the
kriging equation can also be expressed in terms of the semi-variogram as
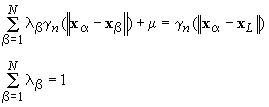 (9)
(9)
where we have
used normalized semi-variogram, i.e., semi-variogram normalized by C(0)
as we did in deriving Eq. (8).
Having obtained the weighting
coefficients (![]() ) and the
Lagrangian coefficient (
) and the
Lagrangian coefficient (![]() ) by solving
either Eq. (8) OR Eq. (9), the kriging variance, Eq. (6), can be expressed as:
) by solving
either Eq. (8) OR Eq. (9), the kriging variance, Eq. (6), can be expressed as:
 (10)
(10)
The above equations are the
basis of the Easykrig software package.
1.1.2
Brief description of EasyKrig3.0
The
EasyKrig program package uses a Graphical User Interface (GUI).
It requires MATLAB 5.3 or higher with or without optimization
toolbox (see section 2.2) and consists of five components, or processing
stages: (1) data preparation, (2) variogram computation, (3) kriging, (4)
visualization and (5) saving results. It allows the user to process anisotropic
data, select an appropriate model from a list of variogram models, and a choice of kriging methods, as well as
associated kriging parameters, which are also common features of the other
existing software packages. One of the major advantages of this program package
is that the program minimizes the users' requirements to "guess" the
initial parameters and automatically generates the required default parameters.
In addition, because it uses a GUI, the modifications from the initial
parameter settings can be easily performed. Another feature of this program
package is that it has a built-in on-line help library that allows the user to
obtain the descriptions of the use of parameters and operation options easily.
The
current EasyKrig3.0 is the upgraded version of the previous version
(EasyKrig2.1). In addition to having corrected some programming errors in the
previous version (mostly GUI related errors), there are many new features
included in the current version:
- Matlab Version 6.x and 7.0 (tested under Windows) compatible
- Capable of handling 3-D data
- Enhanced batch file processing capability
- More flexible in loading input data and saving output data
- Capable of handling the customized grid file
- More examples with detailed step by step instructions are provided to allow user(s) to master the functionality of the software package more quickly and easily.
Although
this software package lacks some abilities such as Co-kriging, it does provide
a convenient tool for geostatistical applications and should also help
scientists from other fields.
For people who do not want to
use GUI but only interested in function-based m-files can go to a different
website that provides a function-based m-file Kriging package (http://globec.whoi.edu/software/kriging/V3/intro_v3.html)
developed by Caroline Lafleur and Yves Gratton, INRS-Océanologie, Universit du
Qubec Rimouski.
1.2
Getting Started
1.2.1
Operating systems
The
software was originally developed under MATLAB 6.5 on a PC (windows 2000) and
intended to be computer and/or operating system independent. The program has
been tested on various machines (PC,
Macintosh, and Sun Workstation) and operating systems (windows 2000/XP,
Linux) and performs fine.
1.2.2 Down-load the program
The
user needs to download the compressed file from GLOBEC
web site first, the URL is
ftp://globec.whoi.edu/pub/software/kriging/easy_krig/
and the compressed file is:
Windows 95/98/NT/2000/XP, Macintosh and Linux: EasyKrig3.0.zip
Unix:
EasyKrig3.0.tar.gz
After
having downloaded the file, the user needs to uncompress the file. A directory of EasyKrig3.0 will be created
and you are ready to run the program.
1.2.3
Quick start
Start MATLAB and go to the designated EasyKrig3.0 home directory. Just type "startkrig" in the MATLAB command window, a window will pop up. This window is the base window, called the Navigator window. The Menubar in this window contains many options you can choose. Now you are ready to move on.
Note:
You can add the kriging home directory to the Matlab search path and run the
program from other directories. However, you have to make sure that there are
no functions of your own having the same names as those used for EasyKrig3.0.
Since the program will allow you to load and save files using a file browser,
it is recommended that you run the program under the EasyKrig3.0 home
directory.
The
program provides a full on-line help function that provides the descriptions
the use of almost all of the selectable functions, options, and parameters. It
is quite self-explanatory and easy to use.
2. Data
Processing Stages
There
are several data processing stages (tasks) that are selectable from the Menubar
on the top of the Navigator window, as well as other task windows. By selecting
or clicking on any of the tasks, a window corresponding to the selected task
will pop up. On each task window including the Navigator window, the
descriptions and explanations of every option and selection in each task window
can be found by click on the "Help" option on the Menubar. On any of the task
windows, clicking on the "Navigator" button, or selecting "Navigator" from the
Menubar will bring back the Navigator window.
2.1 Data
Preparation
Selecting
"Load Data" from "Task" on the Menubar of any window leads to the Data
Preparation window. Click on the "Load" button or select "Load" from the
Menubar to load the raw data file. The format of the data file should be a
3-column ASCII file for 2D data and 4-column ASCII file for 3D data. Comments at the beginning of the data file
will not affect the data as long as each comment line begins with a percentage
symbol "%".
User(s)
can provide their own m-file to load the data by using "External Program"
option in the Data Preparation window. This function allows the user to
generate the input data directly from the raw data instead of generating an
ASCII file that is required by the Easykrig3.0. The required format for the
input and output parameters by using an external program can be found by
clicking on the "Help" from the Menubar and selecting "External Program".
One can set the other parameters such as
reduction factor (or just accept default settings) before loading the file.
After the file is loaded, if the user wants to change the other (default)
settings, such as data filter, he/she can do so and then click
on "Apply"
pushbutton after the parameters have been set. The difference between "Load"
and "Apply" is that the latter operation is faster since it will not re-load
the data file. For example, to change the
axis labels after having loaded the data, one does not need to re-load the
data.
One can also save the "Data Format" information into a
file, which will save all the parameter and option settings in this window.
This feature allows the user(s) to load the data file with the same settings in
the task window Kriging without opening or using this window. It is very useful
when a batch process operation is needed (see explanation in 2.3 and the
example 3 for more details).
The
usage of the other options in this window can be found by selecting appropriate
items from "Help" option on the Menubar.
2.2
Semi-variogram
Selecting
"Variogram" from "Task" on the Menubar leads to a popup Variogram/Correlogram
window. Click on the "Computer" button to generate a data-based semi-variogram
(or correlogram). Then, we need to seek a model-based semi-variogram or
correlogram to fit the data-based variogram just computed. It can be proved
that, based on Eq. (4), the relation between the normalized semi-variogram
γn(h) [ normalized by the variance C(0)] and the
correlogram Cn(h) is:
Cn(h)
= 1 - γn(h),
where h is the lag distance (Eq. 2). An appropriate variogram/correlogram model can be selected
depending on the shape of the variogram/correlogram computed from the data. The
explanations of the parameters associated with the model can be found using the
on-line help. Click on the "Apply" button and the program will compute the
model-based variogram/correlogram using the current settings. The parameter
settings can be changed either by changing the slider positions or by entering
the numbers directly into the associated text-edit fields. If using the slider,
the theoretical curve will change automatically, while if entering the
number(s) into the text-edit field(s), the user needs to click on the "Apply"
button to re-compute the curve.
If the optimization toolbox
(recommended) is installed, the user can use the Least-Squares Fit function to
fit the data by clicking on the "LSQ fit" button. If the optimization toolbox
isn't installed, the program will automatically disable the Least-Squares fit
function.
Note
that since the LSQ fit has a certain range for each parameter, different
initial settings or parameters will produce different results.
In
some cases when the data are anisotropic, an anisotropic variogram or
correlogram model can be activated. By selecting "Anisotropy" radio option, the
corresponding settings are enabled. If you don't know or are not sure of the
orientation and aspect ratio of the anisotropic feature of the data, you can
use the default settings first and then adjust to obtain satisfactory results.
One
can save the current variogram parameters to a file and can also retrieve the
variogram parameters previously saved to a file.
The
usage of the other options in this window can be found by selecting appropriate
items from "Help" option on the Menubar.
2.3
Kriging
Selecting
"Kriging" from "Task" on the Menubar leads to a popup Kriging window. The
parameters of the variogram or correlogram needed in the kriging operation are
automatically passed from the Variogram window to the Kriging window.
Click
on the "Refresh" button to obtain the most recent semi-variogram and
coordinates parameters if the user has loaded a new data set.
The
"Relative Variance" parameter will set the kriging values to "NaN" (Not a
number) when the kriged values are larger than this parameter and will become
blank in the kriging map. The default value of this parameter is 2.5.
Click
on the "Krig" button to start kriging. In general, accepting the default
parameters will produce a reasonable kriging map to start with. Changing the
variogram and kriging parameters will offer fine-tuning on these parameters and
can further improve the quality of the kriging results.
One
of the important features of the EasyKrig is its ability of performing "Batch
Process", which allows the user to process a group of data sets that have the
same data structures, i.e., having the same data format and using the same
variogram and kriging parameters. The user will provide a file in which a list
of the data file will be included. The outputs of each data set from kriging
will be automatically saved to appropriate file in Matlab binary format.
Another added feature in
EasyKrig3.0 is that it allows users to provide their own grid file to specify
the coordinates of regular or irregular grids on which the kriged values are
generated.
The
usage of the other options in this window can be found by selecting appropriate
items from "Help" option on the Menubar.
2.4
Visualization
Choosing
"Visualization" from "Task" on the Menubar leads to the Visualization window.
Three types of figures can be viewed in this window: kriging map,
kriging-variance map and cross-validation. The first two maps are commonly used
in the kriging literature while the last one is a unique approach of this
program.
Click
on the "Show Plot" button to display the current kriging results.
The
shading option is for the display purpose only and their explanations can be
found by typing "help shading" in the MATLAB command window.
Sliders
next to the colorbar case can be used to change the display range of the
colormap scale. Sliders next to the X, Y, and Y axes in 3D case are used to
change the positions of the slices in
X, Y, and Z directions, respectively.
If
the data have been transformed in the Data Preparation window, the kriging
results are the results from transformed data.
An important feature of the
EasyKrig is it can provide "cross-validation", which can be performed by
selecting the "Validation" radio option. One can compute and display the
results from different cross-validation schemes in a separate Cross-Validation
window. Among these schemes, the Q1 and Q2 are good indicators that provide a
plausible assessment of the performance of the kriging in addition to the
kriging-variance map. More detailed descriptions of these cross-validation can
be found from the built-in "Help" function. In general, the Q1 criterion
(distribution of the deviation for the mean) is easy to satisfy while the Q2
criterion (distribution of deviations for the standard deviation) is much more
difficult to satisfy.
As
a rule of thumb, reducing the area under the theoretical curve of the variogram
(smaller nugget, lower sill, smaller length scale, etc.) will increase the Q2
value, while increasing this area will reduce the Q2 value.
The
usage of the other options in this window can be found by selecting appropriate
items from "Help" option on the Menubar.
2.5
Saving
Kriging Results
In
the Visualization window, by selecting "File" from the Menubar and then
choosing "Save File As", the user can save the outputs to a .mat file with a
user-defined filename and at the user-selected location. The program saves the
parameters and data structures (para and data) in the file. For information on
the structures, the user needs to select "File" from the Menubar in the
Navigator window and then "Variable Structure" to obtain explanations for some
important variables (note that many variables are not relevant to users).
3.
Examples
There
are several sample data files included in the package. All files are in ASCII
format required by the program. In the following examples, the designated
directory is assumed to be "easy_krig3.0".
3.1 Example 1: An Aerial Image of Zooplankton Abundance Data
(1)
Start
MATLAB, in command window, change directory to the home directory of
EasyKrig3.0. Type "startkrig" to launch the program.
(2)
Adjust the
window size and position and select "Save Window Position" option from "Task"
on the Menubar and then "Save Position" from the sub-menu. Note that after
saving the window size and position, any of other task windows created
afterwards will have the same size and at the same position. You can resize and
re-position the window in any other task windows as well.
(3)
Select
"Load Data" from "Task" on the Menubar to open the Data Preparation window.
(a)
Select
"Data Col. 2" from the listbox of
"Column" for X-Axis and "Data Col. 1" for Y-Axis (defaults).
(b)
Select
"LONGITUDE" from listbox of "Variable" for X-Axis and "LATITUDE" for
Y-Axis (defaults).
(c)
Leave other
parameters unchanged.
(d)
Click on
the "Load" button to open a dialog box, go to "data" directory, and then select
the data file "zooplankton.dat" to load the selected file into memory.
(e)
Select
"Sample Sequence" in the "Display Type" frame to display the sample sequence.
By selecting "2D/3D Color-coded View" to bring back the color-coded display.
(4) Select
"Variogram" from "Task" on the Menubar
to open the Variogram/Correlogram window.
(a)
Click on
the "Compute" button to compute the semi-variogram. This plots the data-based
semi-variogram as discrete open circles.
(b)
Select
"general exponential-Bessel" (default) from the variogram model listbox on the
upper right. Click on the "LSQ Fit" button. If you don't have optimization
toolbox, click on the "Apply" button, a theoretical model-based semi-variogram
will be superimposed on the original data-based semi-variogram. The resultant
semi-variogram parameters from the least-squares fit (if you have optimization
toolbox) or from the default settings (if you don't have optimization toolbox)
are shown in the text-edit fields within
the "Model Parameters" frame.
(c)
Click on
the sliders associated with the variogram parameters, the theoretical curves will
change accordingly to reflect the parameter changes. The parameters can also be
changed by entering the values directly into the text-edit fields and then
clicking on the "Apply" pushbutton.
(d)
Type 0 in
the "nugget" text-edit field, 1.0 in the "sill" text-edit field, 0.1 in the
"length" text-edit field, 1.5 in the "power" field, and 0 in the 'hole scl'
(hole scale) text-edit field. Then,
click on the "Apply" button. A revised theoretical curve of the model-based semi-variogram will be generated and plotted
(red curve).
(e)
By
selecting the "Variogram" or "Correlogram" in the "Model Parameter" frame (top
row) will provide either variogram or correlogram depending on the user
selection.
(5) Select
"Kriging" from "Task" on the Menubar to open the Kriging window.
(a) Simply
click on the "Krig" button to start kriging by accepting the default settings. A status window pops up and displays the
processing progress. When the kriging is done, click on the "Quit" button to
close the status window.
(6) Select
"Visualization" from "Task" on the Menubar to open the Visualization
window.
(a)
Simply
click on the "Show Plot" button to display the kriging results. Note that the
station positions on the kriging map are color-coded to reflect the level of
the agreement of the kriged results with the original data. If they are
invisible it is because they agree with the kriged values very well.
(b)
Select
"Faceted" and then "Flat" for the "Shading" to see the changes in the display.
(c)
Click on
"Data" from the Menubar and then select between "Color", "Black/White" and
"None" to observe the color change at the locations of the original data.
Selecting "Value" or "Error" and specifying the "Color" and "Fontsize" allow
the user to display the observed values or the difference between the observed
values and those from kriging.
(d)
Select
"Variance Map" to display kriging variance map.
(e)
Selecting
"Validation" will open a small popup "Validation" window. Click on "Compute"
button, the Q1-validation curve occurs. A vertical red line at about 0.09 in
between the two black lines at about 0.5 and -0.5 indicates the model
parameters are good based on the Q1 criterion.
(f)
Selecting
"Q2" from the listbox of "Method" results in another plot. A vertical red line
is located within the accept region at about 1.09, which means the model
parameters are likely "good" based on the Q2 criterion. Click on "Quit" button to close the
Validation window.
(g)
Activate the "Kriging" window by either selecting "Kriging" from "Task"
on the Menubar, or selecting "Kriging
Configuration" from "Window" on the Menubar, or simply clicking on the
minimized "Kriging Configuration" on the Toolbar at the bottom of the screen.
Type 1.1 in the "Relative Variance" text-edit field and click on "Krig" to perform a new kriging. Note that in the Matlab command window,
there is one line message resulting from kriging "Anomaly_cnt for |Ep| >
Relative Error =37". This is to inform the user that there are 37 kriged values
whose normalized kriging variances or relative errors are greater than 1.1. The
total number of kriged value for this example is 266 (19 x 14), which can be
verified by typing "data.out.krig"
(look for Xg, Yg, Vg, and Eg) in the command window.
(h)
Go back to the "Visualization" window, click on "Krig Map" to refresh the
kriging map. There are blank regions on the kriging map, where the normalized
kriging variance (normalized by the variance) exceeds specified "Relative
Variance", i.e. 1.1.
(7)
Select
"Kriging" from "Task" on the Menubar or simply click on the minimized the
figure on the toolbar at the bottom of the screen to bring back the Kriging
window.
(a)
Change
"Relative Variance" back to 2.5.
(b)
Select
"Customized Grid File" in the "Coordinates" frame and click on "Browse" button
to open a file dialogue box. Load
"globec_grid.dat" from the directory "data/GLOBEC_gridfile".
(c)
Click on
the "Krig" button to perform kriging by accepting the other settings in this
window.
(8) Select
"Visualization" from "Task" on the Menubar or simply click on the minimized the
figure on the toolbar at the bottom of the screen to bring back the
Visualization window.
(a)
Click on
the "Show Plot" button to display the kriging results.
(b)
Select
"Interp" for the "Shading" to changes in the display.
(9) Select "File" the
Menubar and then select "Save File As" to open a dialog box.
(a)
Go to
"output" directory or any directory you like and specify any filename you like
(the default filename is zooplankton.mat) and then click on the "Save" button
to save all the data and parameter structures to a MATLAB binary file.
(b)
Click on
"Quit" from the Menubar and then "Quit Easykrig" to quit the program. Restart
the program again by typing "startkrig" in the MATLAB command window. Click on
the "Visualization" button to open the Visualization window, and click on the
"Load" button or select "File" and then "Load" from the Menubar to load the
output file that has just been saved by using the file browser.
(c)
Click on
the "Show Plot" button to display the kriging results, which should be the same
as before.
(10) Click on "Navigator" button or select
"Navigator" from "Task" on the
Menubar to open the Navigator window.
(a)
Select "About" from the Menubar and then
"Variable Structure" to open the data structure description file. You can view
how the data and para are structured and can extract many parameters such as
variogram parameters related to the kriging outputs.
(b)
Click on "Quit" from the Menubar and
then "Quit Easykrig" to quit the program. Type "cd misc_mfiles" in the Matlab
command window to go to the "misc_mfiles" directory.
(c)
Type
"display_globec_grid" in command window and a load data window pops up.
(d)
Use the file
browser to load the data just saved in step (9)-(a) to view the results.
(e)
You can modify the display_globec_grid.m to
plot the output variables yourself.
3.2 Example
2: A Vertical Section of Salinity Data – An Anisotropic Data set
(1)
Start
MATLAB in the MATLAB command window. Change directory to the home directory of
EasyKrig3.0 and type "startkrig" to launch the program.
(2)
Select
"Load Data" from "Task" on the Menubar to open the Data Preparation window.
(a)
Click on
the "Load" button to open a dialog box, select "data" directory, and then
select "salinity.dat" file to load the selected file into memory.
(b)
Select
"Data Col. 1" and "Data Col. 2" from listbox "Column" for X-Axis and Y-Axis,
respectively.
(c)
Select "X"
and "Depth" from the listbox of "Variable" for X-Axis and Y-Axis, respectively.
(d)
Leave other
parameters unchanged and click on "Apply" button.
(e)
Select
"Reverse" radio option on the Y-Axis column to reverse the y-axis direction.
(3)
Select
"Variogram" from "Task" on the Menubar to open the Variogram window.
(a)
Click on
the "Compute" button to compute the semi-variogram.
(b)
Click on
the "LSQ Fit" button [If you don't have optimization toolbox, go to step (c).]
A theoretical model-based semi-variogram will be superimposed on the original
data-based semi-variogram.
(c)
Type 0 in
the "nugget" parameter text-edit field, 1.28 for "sill", 0.36 for "length",
1.76 for "power", and 0 for "hole scl" (hole scale), and then click on the "Apply"
button to generate a theoretical curve of the model-based semi-variogram.
(4) Select
"'Kriging" from "Task" on the "Task" on the Menubar to open the Kriging
window.
(a) Simply click on the "Krig" button to
start kriging by accepting the default settings.
(5) Select "Visualization" from "Task" on the Menubar to open the
Visualization window.
(a)
Click on
the "Show Plot" button to display the kriging results.
(b)
Verify
that "Reverse" is selected for the y
axis direction.
(c)
Select
"Validation" from "Display" will open a small popup "Validation" window. Click
on "Compute" to obtain the "Q1"value. A
vertical red line around 0.08 in between the two black lines at about 0.1 and
-0.1 indicates the model parameters are good based on Q1 criterion.
(d)
Select "Q2"
from the listbox of "method" results. There is no red vertical line in between
the two black lines defining the Q2-accept region, but a value about 2.27
displayed on the top of the figure, indicating that the Q2 value is beyond the
accept region and the variogram model parameters are likely not "good". As a
result, further modifications to the parameters are needed. Do not close this
Cross-Validation window at this moment.
(6) Go
back to Variogram window by either selecting "Variogram" from "Task" on the Menubar or simply click on the
minimized the figure on the toolbar at the bottom of the screen.
(a)
Select
"Anisotropy" radio option to enable 2D variogram computation.
(b)
Change "End
Angle (deg)" to 180, "Angle Inc. (deg)" to 10, and "Tolerance (deg)" to 20
(these are all default settings).
(c)
Click on
the "Compute" button to compute and display the 2D variogram (image) in a
separate window.
(d)
Since the
variogram image shows an elongated pattern having an aspect ratio of about 1:4
(Y/X) and an orientation angle of about 0 degree. On Variogram window, enter
0.25 in the "Y/X" text-edit field of "Ratio" (inverse of the anisotropic aspect
ratio) and 0 in the "Rotation" text-edit field (default) and then click on the
"Compute" button again. A recomputed 2-D semi-variogram shows basically an
isotropic pattern for the central region (Lag distance in radial direction <
0.3).
(e)
Click on
"Quit" button to close "Display 2D/3D Variogram/Correlogram" window.
(f)
Click on
"Isotropy" radio option to disable the "Anisotropy" (the parameters describing
the anisotropic feature of the data have been already accepted) and click on
the "Compute" button to re-compute the equivalent 1D
semi-variogram obtained by transforming the original anisotropic data to
isotropic data by using the anisotropic parameters "Rotation" and the "Ratio"
set in step (3). This step is necessary to obtain the correct 1-D
semi-variogram that actually used in kriging.
(g)
Adjust
display control by clicking on the two sliders ("Lag" and "Value") below the
graphic window.
(h)
Enter 0.6
in the range text-edit field and click on the "LSQ fit" button. If you don't have optimization toolbox, go to the
next step.
(i)
Change
"nugget" to 0.0165, "sill" to 0.39,
"length" to 0.37, "power" to 1.64 and "hole scl" to 0 by entering the
numbers in the corresponding text-edit fields and then click on "Apply" button.
Adjust the display scale by clicking on the
two sliders below the 1-D semi-variogram graphic window, lag for horizontal
scale and value for vertical scale to get better viewing scales.
(7) Go
back to the Validation window and click on "Re-Compute" button to re-compute Q1
and Q2 values. The new values are 0.014 and 1.01 for Q1 and Q2, respectively,
and are both within the acceptable regions, indicating the variogram parameters
are acceptable.
(8)
Select "Kriging" from "Task" on the Menubar or simply click on the
minimized the figure on the toolbar at the bottom of the screen to bring back
the Kriging window and click on the "Krig" button to re-compute the kriging
map.
(9) Select
"Visualization" from "Task" on the Menubar or simply click on the minimized the
figure on the toolbar at the bottom of the screen to bring back the
Visualization window.
(a)
Click on
"Krig Map" and "Variance Map" to refresh the maps. Note that by using an anisotropic
variogram model, some improvements can be achieved, but the kriging map itself
doesn't change much.
(10)
Select "File" from "Task" on the Menubar and then select "Save File As" to open
a dialog box.
(a)
Select
"output" directory and any name you like (the default filename is salinity.mat)
and click on the "Save" button.
(b)
Click on
"Quit" on the Menubar and then "Quit Easykrig" to quit the program. Restart the
program again by typing "startkrig" in the MATLAB command window.
(c)
Select
"Visualization" from "Task" on the Menubar to open the Visualization window and
click on the "Load" button to load the output file that has just been saved by
using the file browser.
(d)
Click on
the "Show Plot" button to display the kriging results and select the "Reverse"
on y-axis to reverse the y-axis direction. The resultant map(s) should be the
same as before.
3.3 Example
3: Batch Process of Pressure (dbar) at
Different Potential Density Layers
(1)
Start MATLAB in the
MATLAB command window, change directory to the home directory of EasyKrig. Type
"startkrig" to launch the program.
(2) Select
"Load Data" from "Task" on the
Menubar to open the Data Preparation window.
(a)
Select
"Data Col. 2" from the listbox of
"Column" for X-Axis and "Data Col. 1" for Y-Axis (defaults).
(b)
Select "LONGITUDE"
from listbox of "Variable" for X-Axis and "LATITUDE" for Y-Axis (defaults).
(c) Selecting "External Program" enables the external program browser and a filename window appears. Note that the X, Y, and Z axes pushdown menu for "Column" are disabled and can be enabled by de-select the "External Program" radio option.
(d)
Click on the file
browser, change directory to "misc_mfiles" and select "test_remove_nan.m", and
then click on "open" to enable the program to access the program (if this
external program is not chosen, the locations where the data values are NaN's
will be displayed on the map). This program provides an example to write your
own routine to obtain the required data format for EasyKrig from an arbitrary
data file. It should be pointed out that the function of removing NaN’s has
already been included in the default loading data process, this example is
simply to demonstrate how to use the external program to load the data with
customized data manipulations.
(e)
Click on the "Load"
button to open a dialog box, go to
"data/pressure" directory, and then select "layer12.dat" file to load the
selected file into memory.
(f)
Select "Save Data
Format" near the bottom of the window, and use "Browse" to save the data format
to a file. This data format file can be used when the user wants to load and
process data using the same data format but without opening Data Preparation
and "Variogram windows (see step (6) in this example).
(3) Select
"Variogram" from "Task" on the
Menubar to open the Variogram window.
(a)
Click on the
"Compute" button to compute the semi-variogram.
(b)
Select "general
exponential-Bessel" (default) from the variogram model listbox on the upper
right. Click on the "LSQ Fit" button. If you don't have optimization toolbox,
click on the "Apply" button, a theoretical model-based semi-variogram will be
superimposed on the original data-based semi-variogram. The parameters from the
Least-Squares fit (if you have optimization toolbox) or from the default
settings (if you don't have optimization toolbox) are shown in the text-edit
fields within the "Model Parameters" frame.
(c)
Change "nugget" to 0.0, "sill" to 1.0, "length" to 0.24, "power" to 1.5 and "hole scl" to 0 by
entering the numbers in the text-edit fields accordingly, and then click on
"Apply" button.
(4) Select
"Kriging" from "Task" on the Menubar
to open the Kriging window.
(a)
Set coordinates as:
minimum
horizontal to -22
maximum
horizontal to -12
horizontal
resolution to 0.4
minimum
vertical to -25
maximum
vertical to -20
vertical
resolution to 0.2
(b)
Select "Batch
Processing" radio button to enable the batch processing.
(c)
Click on the
"Browse" button next to the "Load Filename-list file" to initiate the file
browser. Change the directory to "data" and select "pressure_batch_file.dat" to
load the filename-list file in which a list of data file names is specified.
(d)
Click on the
"Browse" button next to the "Save batch log file" to initiate the file browser.
Change the directory to "output", or wherever directory you like. Type a
filename for the log file, where the input/output information is saved.
(e)
Click on the "Batch
Krig" button to start batch kriging. The output files will be saved in the same
directory as the batch process log file.
(f)
Select "Save File"
in the "Parameter File" frame to activate the file browser. Click on the
"Browse" pushbutton and specify a filename to save all the parameter settings
including variogram and kriging parameters.
(5) Select
"Visualization" from "Task" on the
Menubar to open the Visualization window.
(a)
Click on the "Show
Plot" button to display the kriging results from the last data set:
"layer14.dat".
(b)
Check the outputs
for the other layers. To check the
processing results, you need to load the output files. Click on the "Load"
button and then change the directory where your log file is saved. Load one of
the output files ("layer10.dat" – "layer14.dat") and display it by click on the
"Show Plot" button.
(c)
If you are not
satisfied with the kriging results, you can go back to the Variogram window
and/or Kriging window to change the involved parameters, and re-kriging until
you are satisfied. For example, by setting nugget=0.05, sill=1.16, length=0.25,
power=1.4, and hole scl=0 in the Variogram window and performing kriging again,
you will obtain a better result, i.e., the resultant Q1 and Q2 will fall within
the acceptable regions. Then go back to the Kriging window and repeat (4)-(f).
(6) Click on "Quit" on the Menubar and select "Quit Easykrig" to quit the program, and then start the program again by typing "startkrig" in the command window.
(a) Select "Kriging" option from "Task" on the Menubar to open the Kriging window.
(b) Select "Load File" in the "Parameter File" frame to activate the file browser. Select "Both parameters" radio option (default) and click on the "Browse" pushbutton to load the parameter file saved in step (4) - (f) in this example.
(c) Select "Load Data Format" radio option at the bottom in the Kriging window and use the activated file browser to load the data format file saved in step (2) – (f) in this example.
(d) Repeat steps (b) – (e) of (4) in this example to perform batch kriging.
(e) Repeat (5) to view the results, which should be the same as before. Note that we don’t need to open the Data Preparation and Variogram windows to obtain the save results.
3.4
Example 4: 3-Dimensional
Temperature Data
(1)
Start MATLAB in the MATLAB command window.
Change directory to the home directory of EasyKrig3.0 and type "startkrig" to
launch the program.
(2)
Select "Load Data" from "Task" on the Menubar
to open the Data Preparation window.
(a)
Select
"Data Col. 2", "Data Col. 1", and "Data Col. 3" from the listbox "Column" for
X-Axis, Y-Axis, and Z-Axis, respectively (defaults).
(b)
Select
"LONGITUDE", "LATITUDE", and "Depth" from listbox of "Variable" for X-Axis, Y-Axis, Z-Axis, respectively (defaults).
(c)
Click on
the "Load" button to open a dialog box, select "data" directory, and then
select "Temperature3d.dat" file to load the data into memory.
(3)
Select
"Variogram" from "Task" on the Menubar to open the Variogram window.
(a)
Click on
the "Compute" button to compute the semi-variogram.
(b)
Click on
the "LSQ Fit" button [If you don't have optimization toolbox, go to step (c).]
A theoretical model-based semi-variogram will be superimposed on the original
data-based semi-variogram.
(c)
Set 0 to
"nugget", 1.73 to "sill", 0.50 to "length", 1.98 to "power", and 0 to "hole
scl" (hole scale), and then click on the "Apply" button. A revised theoretical
curve of the model-based semi-variogram will be plotted.
(4) Select
"Kriging" option from "Task" on the Menubar to open the Kriging window.
(a) Simply
click on the "Krig" button to start kriging by accepting the default settings.
(5) Select "Visualization" from the "Task" on the Menubar to open the
Visualization window.
(a)
Simply
click on the "Show Plot" button to display the 3D kriging results.
(b)
Change the
x, y and z position sliders to view the kriging results with different slice
position combinations. Note that the refreshing time is long because there are
too many color-coded data points. Click on "Data" from the Menubar and select
"None" at the bottom of the pull-down menu to remove the color-coded data. The
graphic refresh rate should be much faster than before when you changing the x,
y and z position sliders again.
(c)
Select
"Validation" from "Display" will open a small popup "Validation" window. Click
on "Compute" to obtain the "Q1"value. A
vertical red line around -0.037 in between the two black lines at about 0.05
and -0.05, indicating the model parameters are good based on Q1 criterion.
(d)
Select "Q2"
from the listbox of "Method" results in
a Q2 plot, where Q2 = 7.61, far beyond the Q2 accept region between 0.93 and
1.07.
(e)
Go back to
Variogram window without closing the Validation window. Set "nugget" to 0.0056,
"sill" to 1.7, "length" to 0.50, "power" to
2.0 and "hole scl" to 0 in the respective edit fields and then click on
"Apply" to accept the changes.
(f)
Go back to
the Validation" window and click on "Re-Compute" button to re-compute Q1 and Q2
values. The new values are -0.00054 and 1.01 for Q1 and Q2, respectively, and
all within the acceptable regions. Note that slight changes in variogram
parameters result in a very large change in Q2 value. However, as we can see
later that the kriging results do not change much.
(g)
Click on
"Quit" button to close the Validation window.
(6) Select
"'Kriging" from "Task" on the "Task" on the Menubar or simply click on the
minimized the figure on the toolbar at the bottom of the screen to bring back
the kriging window.
(a)
Simply click
on the "Krig" button to start kriging by accepting the default settings.
(7)
Go back to
Visualization window and select "Krig
Map", and then click on the "Show Plot" button to display the new 3D kriging
results. Note that there are blank grid cells whose values of the krig variance
are larger than the "Relative Variance"
threshold set in the Kriging window. You can fill these cells up by setting
this value to 3.0, and then re-performing the kriging.
(8)
Select
"Visualization" from the "Task" on the Menubar or simply click on the minimized
the figure on the toolbar at the bottom of the screen to bring back the
Visualization window.
(a)
Click on
the "Show Plot" button to display the new 3D kriging results.
(b)
Change x,
y, and z position sliders to view the kriging results with different
combinations of slice positions.
(c)
Select
"Save Figure As" from the "File" on the Menubar and specify a filename
(Temperature3d.fig) to save the whole figure in a MATLAB .fig file. Note that
the same function is also available in the other task windows.
(9) Select
"File" from the Menubar and then select "Save File As" to open a dialog box.
(a) Select "output" directory and any name
you like (the default filename is Temerature3d.mat) and click on the "Save"
button.
(b) Click on "Quit" from the Menubar and then
"Quit Easykrig" to quit the program. Type "cd misc_mfiles" in the Matlab
command window to go to the "misc_mfiles" directory and then type
"display_3dkrig_results" to view the results.
(10)
View the Matlab figure file saved in (8)-(c).
(a)
Select
"Open" from "File" on the Menubar either from "TEMPERATURE" window (figure No.
1) or "KRIGING VARIANCE" window (Figure No. 2) and load "Temperature3d.fig",
the saved figure is displayed. Note that the options and buttons in the saved
figure file will not work properly since the saved figure will not retain all
the information on any of the processing functions. If you don’t have a GUI-based matlab command window, you can type
"figure" in matlab command window first to open a graphic window, and then select
"Open" from "File" on the Menubar to load "Temperature3d.fig".
4. References
Deutsch, C. V and A. G. Journel, 1992.
GSLIB: Geostatistical Software Library and
User's Guide. Oxford University Press, Oxford, 340 p.
Journel, A.G.
& C.J. Huijbregts, 1992. Mining Geostatistics. Academic Press, New York,
600 p.
Kitanidis,
P.K. 1997. Introduction to Geostatistics. Applications in hydrogeology.
Cambridge University Press. 249 p.
Marcotte, D.
1991. Cokriging with MATLAB. Computers & Geosciences. 17(9):1265-1280.